Contents

Ej1

%Imprimir una tabla formateada (entero y real) de
%l logaritmo natural de los números 10,
%20, 40, 60, y 80.
%Sugerencia: usar el comando fprintf y vectores
x=[10 20 40 60 80]';
resul=[x log(x)];
fprintf('\n Numero Natural log\n')
fprintf('%4i \t %8.3f\n', resul')
clear

 Numero Natural log
  10 	    2.303
  20 	    2.996
  40 	    3.689
  60 	    4.094
  80 	    4.382

Ej2

A=[4 -2 -10;2 10 -12;-4 -6 16];
b=[-10 32 -16]';
x=A\b
clear

x =

    2.0000
    4.0000
    1.0000

Ej3

A=[4 -2 -10;2 10 -12;-4 -6 16];
b=[-10 32 -16]';
[L,U]=lu(A)
x=inv(U)*inv(L)*b
clear

L =

    1.0000         0         0
    0.5000    1.0000         0
   -1.0000   -0.7273    1.0000


U =

    4.0000   -2.0000  -10.0000
         0   11.0000   -7.0000
         0         0    0.9091


x =

     2
     4
     1

Ej4

A=[0 1 -1;-6 -11 6;-6 -11 5]
[v,d]=eig(A)

A =

     0     1    -1
    -6   -11     6
    -6   -11     5


v =

    0.7071   -0.2182   -0.0921
    0.0000   -0.4364   -0.5523
    0.7071   -0.8729   -0.8285


d =

   -1.0000         0         0
         0   -2.0000         0
         0         0   -3.0000

Ej5

A=[1.5-2*i -.35+1.2*i;-.35+1.2*i 0.9-1.6*i];
b=[30+40*i;0.9-1.6*i];
v=A\b;

v
P1=v(1)*(30+40*i)'
P2=v(2)*(20+15*i)'
clear

v =

  -0.1532 +26.5814i
   5.0000 +17.6525i


P1 =

   1.0587e+03 + 8.0357e+02i


P2 =

   3.6479e+02 + 2.7805e+02i

Ej6

hanoi(5,'a','b','c')
% function
% hanoi(n, i, a, f)
% if n > 0
% hanoi(n-1, i, f, a);
% fprintf('mover disco %d de %c a %c\n',n,i,f);
% hanoi(n-1, a, i, f);
% end
clear

mover disco 1 de a a c
mover disco 2 de a a b
mover disco 1 de c a b
mover disco 3 de a a c
mover disco 1 de b a a
mover disco 2 de b a c
mover disco 1 de a a c
mover disco 4 de a a b
mover disco 1 de c a b
mover disco 2 de c a a
mover disco 1 de b a a
mover disco 3 de c a b
mover disco 1 de a a c
mover disco 2 de a a b
mover disco 1 de c a b
mover disco 5 de a a c
mover disco 1 de b a a
mover disco 2 de b a c
mover disco 1 de a a c
mover disco 3 de b a a
mover disco 1 de c a b
mover disco 2 de c a a
mover disco 1 de b a a
mover disco 4 de b a c
mover disco 1 de a a c
mover disco 2 de a a b
mover disco 1 de c a b
mover disco 3 de a a c
mover disco 1 de b a a
mover disco 2 de b a c
mover disco 1 de a a c

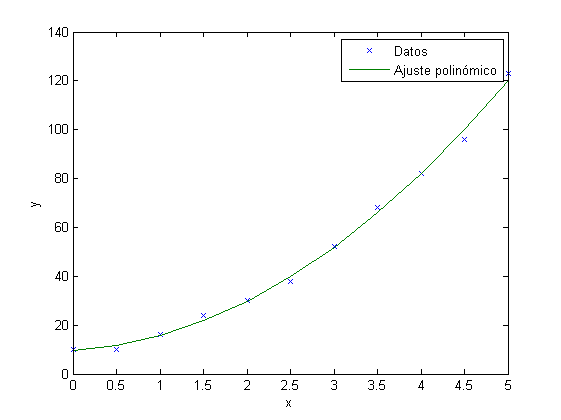
Ej7

%polyfit, polyval

x= 0:0.5:5;
y=[10 10 16 24 30 38 52 68 82 96 123];
p=polyfit(x,y,2);
yc=polyval(p,x);
plot(x,y,'x',x,yc);
xlabel('x'),ylabel('y')
legend('Datos','Ajuste polinómico')
clear

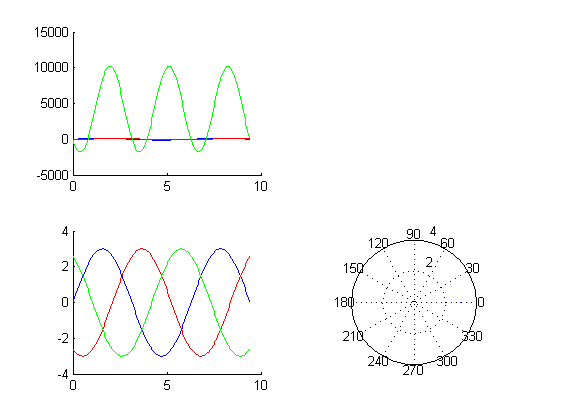
Ej8

wt= 0:0.05:3*pi;
v=120*sin(wt);
i=100*sin(wt-pi/4);
fm=3;
fa=fm*sin(wt);
fb=fm*sin(wt-2*pi/3);
fc=fm*sin(wt-4*pi/3);
subplot(2,2,1)
hold on
plot(wt,v)
plot(wt,i,'r')
plot(wt,v.*i,'g')
subplot(2,2,3)
hold on
plot(wt,fa)
plot(wt,fb,'r')
plot(wt,fc,'g')
subplot(2,2,4)
polar(2*pi,3)

clear

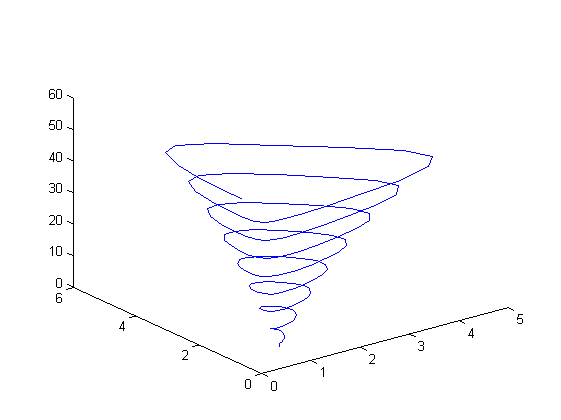
Ej9

t=0:pi/10:16*pi;
x=exp(-0.03*t.*cos(t));
y=exp(-0.03*t.*sin(t));
z=t;
subplot(1,1,1)
plot3(x,y,z)
clear

Ej10

[x,y] = meshgrid(-4:0.3:4,-4:0.3:4);
surf(x,y,sin(x).*cos(y).*(exp(-sqrt(x.^2+y.^2))))
clear

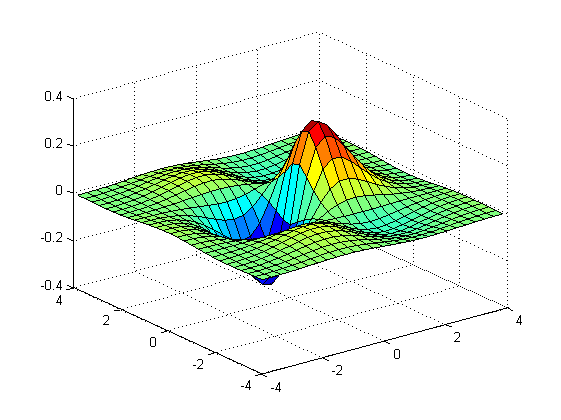
Ej11

%fx=x^4-35*x^2+50*x+24;
fx=[1 0 -35 50 24];
raices=roots(fx)
clear

raices =

   -6.4910
    4.8706
    2.0000
   -0.3796

Ej12

% function
% y = HalfSine(t, y, z)
% h =
% sin
% (
% pi
% *t/5).*(t<=5);
% y = [y(2); -2*z*y(2)-y(1)+h];
[t, yy] = ode45(@HalfSine, [0 35], [1 0], [], 0.15);
plot(t, yy(:,1))
clear

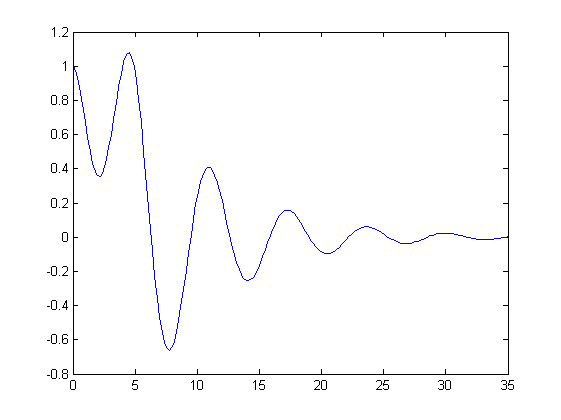
Ej13

Bo = 5;
fo = 10;
ts =0:1/(100*fo):4/fo;

g=  Bo*sin(2*pi*fo*ts)+Bo/2*sin(2*pi*fo*2*ts);
plot(linspace(-1,1,length(g)),abs(fft(g))/length(g))
xlabel('frecuencia ang (x Pi rad)')
clear

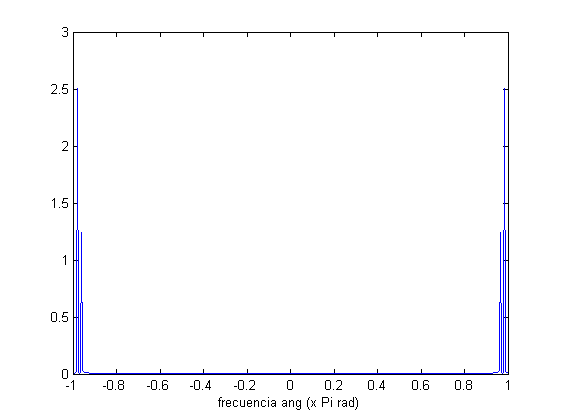
Ej14

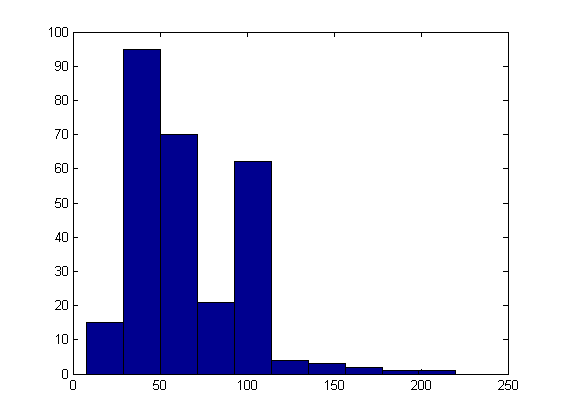
 x = imread('WindTunnel.jpg');
 image(x)

 %f = input('Introducir fila ');
 f=200;
 red = x(f, :, 1);
 gr  = x(f, :, 2);
 bl  = x(f, :, 3);
 figure(1)
 plot(red, 'r');
 figure(2)
 hist(double(red))
 clear

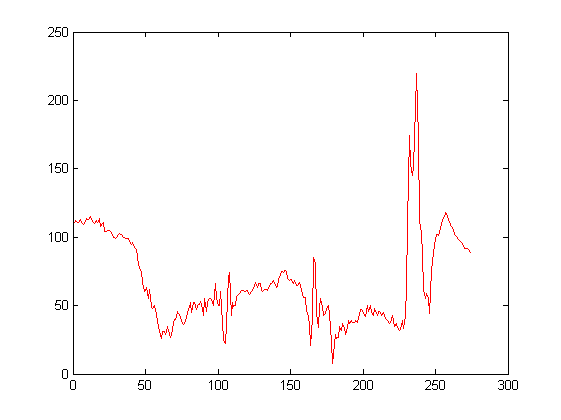
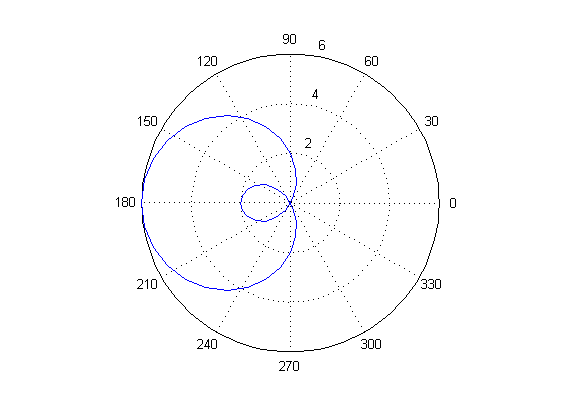
Ej15

theta=-pi:pi/20:pi;
r=2-4*cos(theta);
polar(theta,r)

clear


Published with MATLAB® R2013b

Volver